Propagation of Error and the Reliability of Global Air Temperature Projections, Mark II.
Propagation of nonsense – part II
I thought I would look again at Pat Frank’s paper that we discussed in the previous post. Essentially Pat Frank argues that the surface temperature evolution under a change in forcing can be described as
![\Delta T(K) = f_{CO2} \times 33K \times \left[ \left( F_o + \sum_i \Delta F_i\right) / F_o \right] + a,](https://s0.wp.com/latex.php?latex=%5CDelta+T%28K%29+%3D+f_%7BCO2%7D+%5Ctimes+33K+%5Ctimes+%5Cleft%5B+%5Cleft%28+F_o+%2B+%5Csum_i+%5CDelta+F_i%5Cright%29+%2F+F_o+%5Cright%5D+%2B+a%2C&bg=ffffff&fg=333333&s=0 "\Delta T(K) = f_{CO2} \times 33K \times \left[ \left( F_o + \sum_i \Delta F_i\right) / F_o \right] + a,")
where 
is an enhancement factor that amplifies the GHG-driven warming, 
is the total greenhouse gas forcing, 
is the incremental change in forcing, and 
is the unperturbed temperature (which I’ve taken to be 0).
is an enhancement factor that amplifies the GHG-driven warming, is the total greenhouse gas forcing, is the incremental change in forcing, and is the unperturbed temperature (which I’ve taken to be 0).
Pat Frank then assumes that there is an uncertainty, 
, that can be propagated in the following way
, that can be propagated in the following way
which assumes an uncertainty in each time step of 
and leads to an overall uncertainty that grows with time, reaching very large values within a few decades.
and leads to an overall uncertainty that grows with time, reaching very large values within a few decades.
Since I’m just a simple computational physicist (who is clearly has nothing better to do than work through silly papers) I thought I would code this up. That way I can simply run the simulation many times to try and determine the uncertainty. Since it’s not quite clear which term the uncertainty applies to, I thought I would start by assuming that it applies to 
. However, is constant in each simulation, so I simply randomly varied by 
, assuming that this variation was normally distributed. I also assumed that the change in forcing at every step was 
.
The result is shown in the figure on the upper right. I ran a total of 300 simulations, and there is clearly a range that increases with time, but it’s nothing like what is presented in Pat Frank’s paper. This range is also really a consequence of the variation in 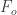ultimately being a variation in climate sensitivity.
ultimately being a variation in climate sensitivity. 
The next thing I can do is assume that the applies to . So, I repeated the simulations, but added an uncertainty to at every step by randomly drawing from a normal distribution with a standard deviation of . The result is shown on the left and is much more like what Pat Frank presented; an ever growing envelope of uncertainty that produces a spread with a range of 
K after 100 years.
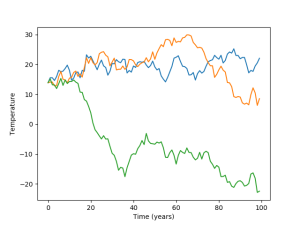Given that in any realistic scenario, the annual change in radiative forcing is going to be much less than 
, Pat Frank is essentially assuming that the uncertainty in this term is much larger than the term itself. I also extracted 3 of the simulation results, which I plot on the right. Remember, that in each of these simulations the radiative forcing is increasing by 
per year. However, according to Pat Frank’s analysis, the uncertainty is large enough that even if the radiative forcing increases by in a century, the surface temperature could go down substantially.
Pat Frank’s analysis essentially suggests that adding energy to the system could lead to cooling. I’m pretty sure that this is physically impossible. Anyway, I think we all probably know that Pat Frank’s analysis is nonsense. Hopefully this makes that a little more obvious.
